 Infinity
Infinity 

 Infinity
Infinity 
Interesting numbers --- zero --- one --- complex --- root 2 --- golden ratio --- e --- pi --- googol --- infinity
The symbol for infinity is like an eight on its side. It represents infinity, since you can go round and round the symbol without ever finding a place to stop. A circle would do this as well, but a circle represents zero and you can't lie a circle on its side in such as obvious way. You definitely don't want to get infinity and zero confused for each other!
What is infinity? It is bigger than the biggest number, but it is not a number itself. You can say
1 / 0 = 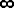 and
2 / 0 =
and
2 / 0 = 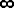
If you could do arithmetic using infinity, then you would end up proving that 1 = 2, which is not a good idea! So you cannot do arithmetic using infinity. It's where the number system breaks down.
So how can we say anything about infinity at all? In fact, we can say more than you'd think. First, we can say that there are infinitely many natural numbers. Now we have a way of counting infinite sets of numbers. Wait a minute - how can we count something that's infinite? Surely it would take a infinite amount of time, even for a computer? Yes, but what does counting mean? If there are seven apples, we count them by saying "1,2,3,4,5,6,7". We put the apples in one-to-one correspondence with the natural numbers. We run out of apples at seven, so that's how many apples there are. So we know that there are infinitely many natural numbers, and if we can put any other set of numbers in one-to-one correspondence with the naturals, then there must be the same 'number'. (Number is in inverted commas, since the number is infinite, which is not a number!)
So let's think of a set of numbers. How about the rationals? Surely there are more rationals (fractions) than natural numbers. After all 2/1 is as much a rational as 1/2. So for every natural number, there is a corresponding rational, and there are a lot more rationals as well. Well, let's see if we can place them in one-to-one correspondence with the natural numbers. First lay out the rationals in a table. The rows give the rationals with the same numerator (top) and the columns give the rationals with the same denominator (bottom). If you carried on writing rows and columns for ever, you would cover all rationals, and none would be left out. This is rather unmathematical language. It would be better to say that any rational that you can think of will be in this table, and you can say exactly where. Now can we go through this table one at a time, and guarantee to cover any number within the table sooner or later? If we can, we have placed the rationals in one to one correspondence with the naturals. Try clicking the button to see if we can.
|
|
As you can see, we can. (The table is laid out as a square, so some of the numbers are off the edge when we go through the table in this way. But keep clicking, and the high-lighted square will reappear.)
You may feel that while we are managing to 'count' the rationals, we are still getting through the rationals slower than the natural numbers. This doesn't matter. We can say definitely that any rational will be counted sooner or later. So the set of rationals is the same size as the set of natural numbers.
Are all infinite sets of numbers the same size? No. The set of irrationals and the set of reals are not countable. There is no way that you can lay them out so there is a one-to-one correspondence with the natural numbers. This means that there are different types of infinity. The countable sets of natural numbers and rationals are smaller than the sets of irrationals and reals.
How many prime numbers are there? A number is a prime if its only factors are itself and one. The nujmber one itself is considered not to be a prime. Click on the button to see the first prime numbers.
You can see that the prime numbers start close together, but then they start getting further and further apart. Is there a biggest prime number, or do they go on for ever? We can prove that the set of prime numbers is infinite. First, let's assume that the set is finite. That means that we could write down every single prime number. (In fact, we probably couldn't as there might be too many to write down in one person's lifetime! But mathematicians can handle the difference between the difficulty of writing down a set of numbers because it is very big, and the impossibility of writing them because the set is infinite). Now, if we could write every prime number, then we could, theoretically, multiply them all together. This result will have all the known primes as factors. Now add one to it. This new number will have none of the known primes as factors. So either it will be a new prime, or it will have at least one new prime as a factor. So it is impossible to write down every single prime. So the set of prime numbers must be infinite.
© Jo Edkins 2007 - Return to Numbers index